Эпитрохоида? Это совсем просто...
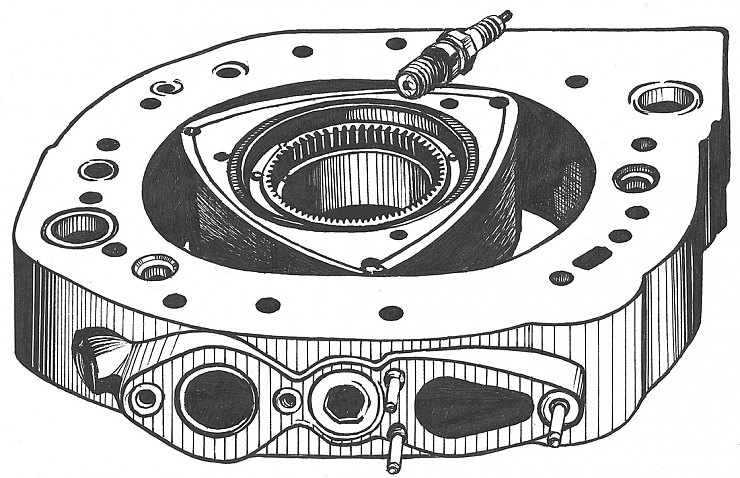
Сколько лет прошло со дня создания роторно-поршневого двигателя (РПД), детища двух талантливых инженеров Феликса Генриха Ванкеля и Вальтера Фройде... А со времени зарождения идеи – еще больше. И все эти долгие десятилетия красивую и строгую линию эпитрохоиду упорно называют «сложной кривой»...
Вот пара примеров. Аркадий Алексеев, статья «Семьдесят лет из жизни "Ванкеля"», «За рулем» № 2/1998. «Однако главную трудность представляет изготовление такого цилиндра: его основанием служит эпитрохоида – сложная геометрическая кривая. Понятно, реализовать это смогли лишь через несколько лет, когда развитие технологии позволило делать поверхности столь сложной формы».
Не оригинален и Максим Сачков, статья «Линия жизни – эпитрохоида», «За рулем» № 7/2001. «В блоке цилиндров – статоре, внутренняя поверхность которого представляет сложную кривую – эпитрохоиду, вращается ротор».
И ни малейшей попытки разобраться и объяснить – что же в ней такого сложного, в эпитрохоиде? А ведь ничего особенного там нет, и мы это сейчас продемонстрируем. Как говорится, следите за руками, здесь даже голову особенно включать не придется.
Вооружимся проверенным методологическим приемом «от простого к сложному». Возьмем пару геометрических объектов – прямую и окружность. Кстати, прямую тоже можно считать окружностью с бесконечным радиусом (R = ∞). И начнем двигать один объект относительно другого.
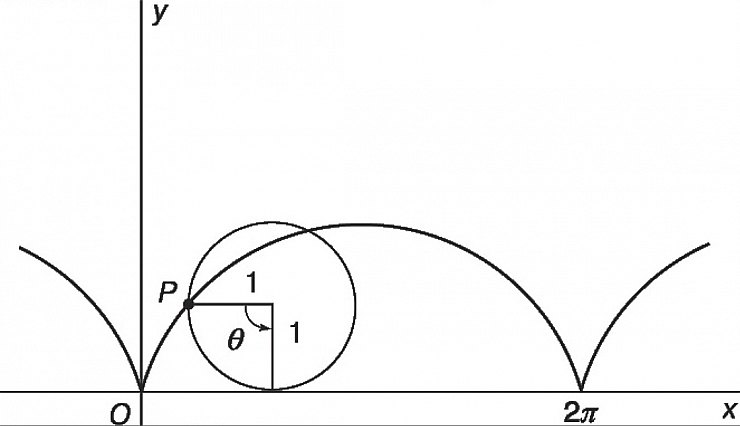
Случай первый. Берем прямую и катим по ней окружность – причем без скольжения. Иными словами, двигаем «R по ∞)». Какую линию прочертит точка на окружности? Конечно, старую добрую циклоиду (рис. 1). Пример в автомобиле – траектория крайней точки на шине. Запомним и вернемся к нашим объектам.
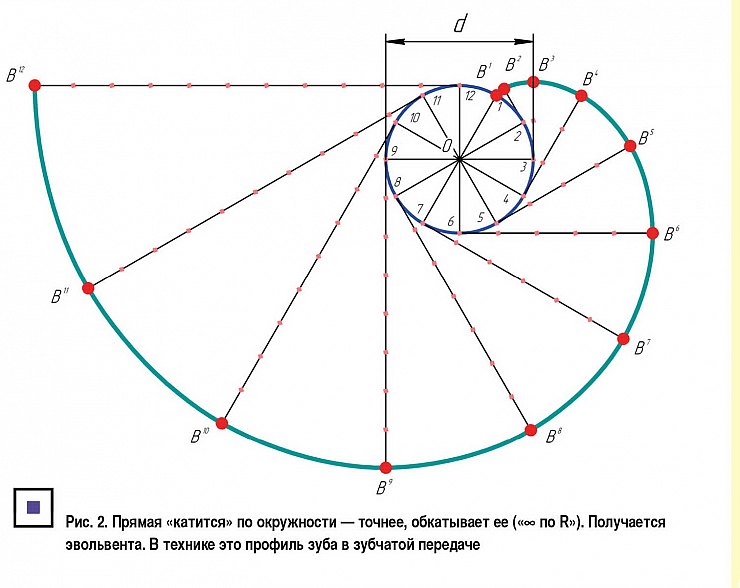
Случай второй. Теперь возьмем прямую и начнем «катать» ее по окружности. Точнее – обкатывать этой прямой окружность, и обязательно без скольжения! Теперь мы двигаем «~ по R». Кривая, которую описывает точка на прямой, называется эвольвентой окружности (рис. 2). Пример в автомобиле, да и вообще в технике – профиль зуба в зубчатом зацеплении.
И наконец, случай третий, он же самый интересный. Возьмем не прямую и окружность, а две окружности. То есть не «R и ∞)», а пару «R и r». И начнем обкатывать окружность радиуса r другой окружностью – с радиусом R.
В общем случае точка на подвижной окружности будет описывать эпициклоиду или гипоциклоиду – в зависимости от того, «кто по кому катится». И «где катится» – снаружи или внутри. Но так или иначе, это будет не «радиус по бесконечности» (как в случае циклоиды), и не «бесконечность по радиусу», (как в случае эвольвенты), а «радиус по радиусу»! Запомним и двинемся дальше.
Прикрепим к подвижной окружности стержень – жестко прикрепим. Неподвижно! Скажем так – приварим! Так вот, точка на этом стержне будет описывать кривую, называемую эпитрохоидой или гипотрохоидой. Но мы будем пользоваться термином эпитрохоида.

А теперь посмотрим на рис. 3, где дан роторно-поршневой двигатель в разрезе. Окружность R катится по другой окружности радиуса r. А точка 1, жестко связанная с подвижной окружностью R, описывает эпитрохоиду. И точка 2 описывает эпитрохоиду, и точка 3 тоже ее, родимую. Вот вам и автомобильное применение эпитрохоиды – профиль камеры сгорания двигателя Ванкеля.
На самом деле все рассмотренные линии – и классическая циклоида, и эпициклоида, и гипоциклоида, и эвольвента, и эпитрохоида – геометрические родственницы. И описываются схожими уравнениями. Все дело лишь в том, «кто по кому катится» – окружность по прямой, прямая по окружности или окружность по окружности.
Так что ничего сложного в эпитрохоиде нет. Как и в ее воспроизведении на станке с ЧПУ. Правда, с одной оговоркой. Раньше, когда такие станки оснащались линейно-круговыми интерполяторами, эпитрохоиду заменяли цепочкой дуг окружностей и отрезков прямых. В математике такая замена называется аппроксимацией.
Точность аппроксимации сказывалась на точности результата. Для приемлемой цифровой модели эпитрохоиды приходилось увеличивать число дуг, а это сказывалось на времени прохождения инструмента по контуру – оно существенно возрастало. С появлением сплайн-интерполяции и микропроцессорного управления станками получение «хитроумных» контуров существенно упростилось. Но это уже совсем другая история.


